何回か読みなおしては少しずつ学んでいる統計学。先日入門書見てもさっぱりんちょだったのでマンガでわかる統計学を買って読んでみた。

なるほどわからん。

マンガと言えども数式と専門用語が一杯で萎えてきた。とりあえず、ここまでは分かったのでメモする。ブログにアウトプットすれば少し理解が深まるだろう(←追記：記事書き終わってちょっと深まった)

統計学ってなんなんよ？

基本的な事を理解すれば、マーケティングデータ分析、金融商品のリスクとリターン、株のボラティリティ、など、いろいろ使い道があるっている学問です。

身近な所だと先日あった選挙。選挙速報ってあるじゃないですか？開票率1%でも当選確実って出せるのは統計学による推測統計というもの。これは比較的新しいやり方で、その前は記述統計と呼ばれるものが主流だったそうです。棒グラフ(ヒストグラム)からある特徴を導き出すとかですね。記述統計も推測統計も一部の事実から全体を把握するというのがその目的で、記述統計に対し、推測統計は確率理論がミックスされた、未来を読み取る方法と言うことで注目されています。

沢山のデータからある特徴を導き出す

世の中いろいろなデータがあります。天気で言えば住んでる場所、日本、アジア、世界まで広げると膨大な数になる。そういう一つ一つのデータを全部確かめて明日の天気を予想してるわけじゃない。

ちょっと話が大きいので、例えば高校のクラスのある教科のテストのデータが以下だったりする。

あるテストの点数

48	54	47	50	53	43	45	43
44	47	58	46	46	63	49	50
48	43	46	45	50	53	51	58
52	53	47	49	45	42	51	49
58	54	45	53	50	69	44	50
58	64	40	57	51	69	58	47
62	47	40	60	48	47	53	47
52	61	55	55	48	48	46	52
45	38	62	47	55	50	46	47
55	48	50	50	54	55	48	50

これから特徴を見出すにはステップがあります。最もポピュラーなやり方はヒストグラムを作ること。そのためには度数分布表を作成します。

度数分布表は記述統計の基本。ヒストグラムで可視化

度数分布表
階級	階級値	度数	相対度数	累計度数
40	38	3	0.038	3
45	43	11	0.138	14
50	48	33	0.413	47
55	53	19	0.238	66
60	58	7	0.088	73
65	63	5	0.063	78
70	68	2	0.025	80

どういうステップでこの度数分布表を作るかと言うと、以下ステップになります。

・データの中から最大値と最小値を取る
・その数値を少範囲に5-8程度分ける→階級
・階級値の真ん中→階級値
・階級に入るデータの数→度数
・度数の全体に対する割合→相対度数
・度数の合計→累計度数

これを元にX軸をテストの点数の階級値、Y軸をその点数を取った人の度数でヒストグラムに表すと以下になる。赤の三角は平均値。

数字の羅列が可視化されてわかりやすくなります。

ふーん。で？

ここまでだと「ふーん、で？」という事になるので、ヒストグラムは事実を可視化したに過ぎないに留めておきます。人々が知りたいのはもっと違うこと。例えば好きな女の子のAさんの点数。じゃなくて、いや、近いのだけども、要はどこに数字がまとまっててと言う事よりも、ばらついている具合だったりします。

昔、偏差値ってあったじゃないですか？

偏差値60だとやや頭がいい。70だとすごい頭がいい。逆も然り。あれもいわゆる統計。平均点より10点上だからオレはすごい！とは必ずしも言えない。限りなく平均より低いグループがそのクラスにいて、普通の子はそれなりに勉強すれば**点以上の点数をとってる人がほとんど。と言う事がバレるのが偏差値です。つまり数字のばらつきの具合を数値化したものです。

標準偏差

偏差値は平均点で50を与え、標準偏差と呼ばれる数字のバラつきの尺度で10を加えたり20を加えたりします。

偏差値70がすごいのは20を与えられているからであって、良い点を取っているグループの更に良い点数を取っているということになります。逆に考えると40も60も大差がないと言うことらしいです。それ高校の時知りたかったなぁ。まあ知ってどうするの的な感じだけど。そういうことらしいです。

階級	度数	偏差
40	3	-12.44
45	11	-7.44
50	33	-0.44
55	19	2.56
60	7	7.56
65	5	12.56
70	2	17.56	3.04	←標準偏差

上の例だと、標準偏差が3.04なので、平均点が50点とすると47-53点に人が集中してて、それ以上、つまり標準偏差の2倍以上離れている人は稀な方だよということが示せるわけです。月並みなのか特殊なのかがわかります。

いつの間にか偏差値の話にそれましたが統計の話。

ここからが本題なんだけど、統計は推測統計という手法があり未来を予測すると上の方で書きましたが、ここから話が繋がります。ただ、話を繋げたいけど自分の頭の理解がまだついていないので簡単に書きます。

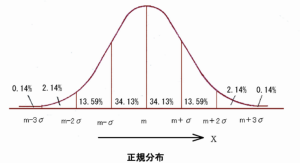
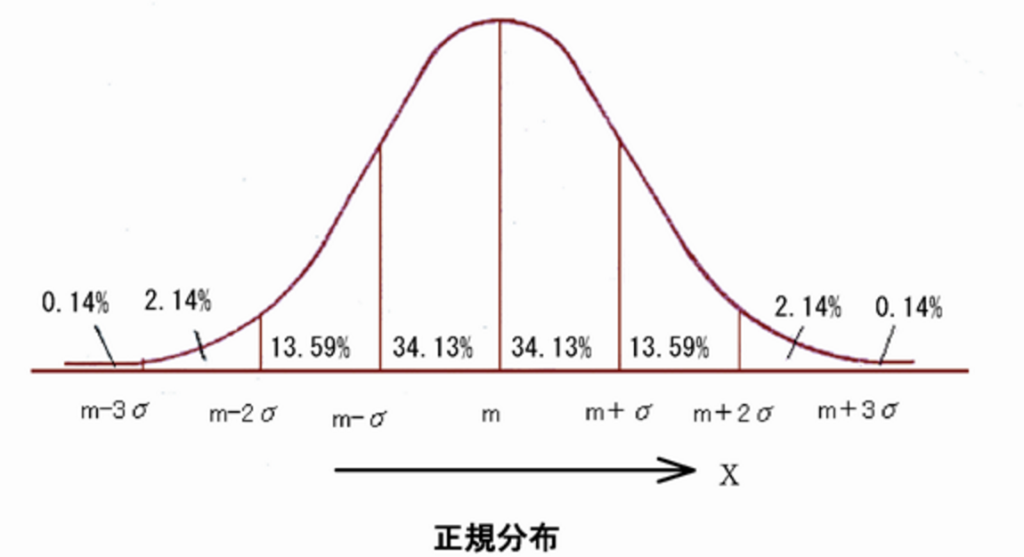
最もよく見かけるデータの集まりとして正規分布があります。先ほどのテストの点数、今度は世界中の人が同じテストを仮に受けたとして、先程のようなグラフを作れるでしょうか？10クラス分ぐらいの人数の点数なら全部数字とって出せますが、1億人以上の膨大な分母だとしたら？無理ですよね。

ヒストグラムの棒の幅をうんと狭めると上のように山の形をした曲線で描かれ確率密度関数と言います。階級の幅が無限に近いと、結果こうなるみたいですね。もちろんこの形は調査対象によって並が違います。ただ、ある公式に当てはめて、それが証明できるならば、上のような「正規分布に従う」ということが言え、少ない母数でも膨大な母集団のデータを取った結果でもさほど変わりのないデータになるという事が言えます。

世界中の人が同じテストを受けた結果を推測する事も可能というわけです。もちろん一部の国だけが異常に離れた数値が出ることもあります。それを求めるのが確率理論で、一番はじめに書いた通り、確率理論と従来の統計をミックスさせたのが推測統計ということになります。統計を取る母集団はデータが膨大になるので、代わりに標本と呼ばれる母集団から抽出されたものを調査して、母集団全体を推測する、それがすなわち統計です。

選挙速報の話もここにつながります。選挙区Xは平均うんたらかんたらで標準偏差が〜の正規分布に従うため、開票率1%の数値であっても当選確実が出せちゃうわけです。ちなみにあれは95%の確率って知ってました？

自分の頭で理解できているのはまだここまで。

いじょ！